Answer:
Explanation:
To prove that this triangle is a right triangle, we need to check the side lengths using pythogoras theorem.
Given:
- Longest side = 25 units
- Triangle side lengths: 25, 15x, and 20x
Putting the side lengths into pythogoras theorem:
- ⇒
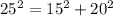
- ⇒
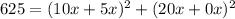
Using the formula "(a + b)² = a² + 2ab + b²
Divide both sides by 625:
The value of x that proves this triangle a right triangle is 1.