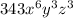Answer:
First, apply the power of a product rule by which you raise each factor to the power 3, and then multiply all the factors, to obtain:
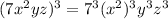
Next, apply the power of a power rule, in virtue of which you raise the factor x² to the power 3 and obtain:
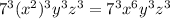
Finally, compute the numerical values, doing 7³ = 7×7×7 = 343.
Therefore, the final result is:
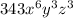
Step-by-step explanation:
The expression you have to simplify is:
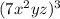
You have to apply two rules:
1. Power of a product
This rule states that the power of a product is equal to the product of each factor raised to the same exponent of the whole prduct:
For instance:
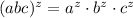
Using this with the expression
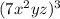 it is:
it is:
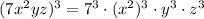
In complete sentences that is: raise every factor, 7, x², x, and z to the exponent 3 and, then, multiply them.
2. Power of a power:
This rule states that to raise a power to a power, you must multiply the exponents.
For instance:
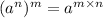
You must apply that rule to the factor
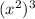
That is:
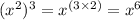
3. Final result and description using complete sentences:
The first step is to apply the power of a product rule by rasing each factor to the power 3, and then multiply all the factors, to obtain:
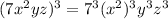
The second step is to apply the power of a power rule, in virtue of which you raise the factor x² to the power 3, in this way:
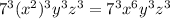
The last step is to calculate the numerical values, doing 7³ = 7×7×7 = 343.
The final result is: