Question

Which equation represents the area of one base of a cylinder if the radius is doubled?

Answer 1

If the radius is doubled, then the area of one base of a cylinder quadrupled and the equation is:

`\boxed{A_(b1)=4\pi r^2}`

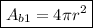
Step-by-step explanation:

The surface area of a solid is the total area of its outer surface. For a cylinder whose radius of its circular base is
`r`, and height
`h`, then the surface area (S) can be calculated as:

`S=\text{Surface area of base 1}+\text{Surface area of base 2}+\text{Surface area of the side} \\ \\ S=A_(b1)+A_(b2)+A{s} \\ \\ S=\pi r^(2)+\pi r^(2)+2\pi rh \\ \\ S=2\pi r^(2)+2\pi rh \\ \\ \\ Because: \\ \\ \text{Surface area of base 1}=\text{Surface area of base 2} \\ \\ \\ Where: \\ \\ A_(b1):\text{Surface area of base 1} \\ \\ A_(b2):\text{Surface area of base 2} \\ \\ A_(s):\text{Surface area of the side}`

So, if the radius is doubled then the area of one base is:

`A_(b1)=\pi (2r)^(2) \\ \\ A_(b1)=\pi (4r^2) \\ \\ \boxed{A_(b1)=4\pi r^2}`