Question

Which of the following is an odd function?

Answer 1

Given:

`f(x)=x^(3)+5 x^(2)+x`

`f(x)=√(x)`

`f(x)=x^(2)+x`

`f(x)=-x`

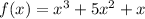
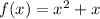
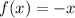
To find:

The odd function.

Solution:

If f(-x) = -f(x), then the function is odd.

If f(-x) = f(x), then the function is even.

Option A:
`f(x)=x^(3)+5 x^(2)+x`

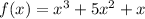
Substitute x = -x

`f(-x)=(-x)^(3)+5 (-x)^(2)+(-x)`

`=-x^3+5x^2-x`

`=-(x^3-5x^2+x)`

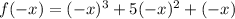
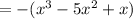
≠ - f(x)

It is not odd function.

Option B:
`f(x)=√(x)`

Substitute x = -x

`f(-x)=√(-x)`

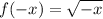
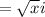`=√(x) i` (Since
`√(-1) =i`)

≠ - f(x)

It is not odd function.

Option C:
`f(x)=x^(2)+x`

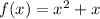
Substitute x = -x

`f(-x)=(-x)^(2)+(-x)`

`=x^2-x`

`=-(-x^2+x)`

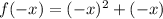
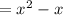
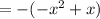
≠ - f(x)

It is not odd function.

Option D:
`f(x)=-x`

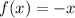
Substitute x = -x

`f(-x)=-(-x)`

`=-f(x)`

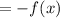
It is odd function.

Therefore, f(x) = -x is an odd function.