Given:
Perpendicular line:
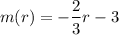
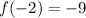
To find:
The equation of the linear function f.
Solution:
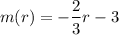
Slope of line m is =

If two lines are perpendicular then the slope of one equation is negative reciprocal of the other.
Slope of line f =

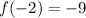
This means f has point (-2, -9).
Using point-slope formula:

Here
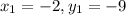 and
and
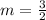
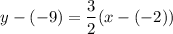

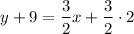
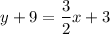
Subtract 9 from both sides.
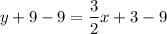

Substitute x = r and y = f.
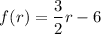
The linear equation is
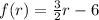 .
.