Answer:
Hence, the coordinate of point P is
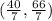 .
.
Explanation:
Given that,
AB is the line segment having endpoints are A and B.
Coordinate of point A is
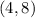 and coordinate of point B is
and coordinate of point B is
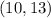 .
.
Point P lies on line segment AB which divides the line segment AB in the 2:5.
Let, the coordinate of point P which divides the line segment AB is
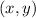 .
.
Now,
The coordinate of a point P, which divides the line segment AB internally in the ratio
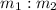 are given by:
are given by:

 coordinate of point P is
coordinate of point P is
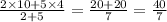
 coordinate of point P is
coordinate of point P is
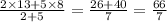
Hence, the coordinate of point P is
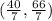 .
.