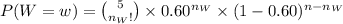Answer:
(a) The joint PMF of W, L and T is:
![P(W,\ L,\ T)={5\choose (n_(W)!* n_(L)!* n_(T)!)}* [0.60]^{n_(W)}* [0.30]^{n_(L)}* [0.10]^{n_(T)}](https://img.qammunity.org/2021/formulas/mathematics/college/ltzb567cm95gn2jol84duigbwodjfg3pq1.png)
(b) The marginal PMF of W is:
Explanation:
Let X = number of soccer games played.
The outcome of the random variable X are:
W = if a game won
L = if a game is lost
T = if there is a tie
The probability of winning a game is, P (W) = 0.60.
The probability of losing a game is, P (L) = 0.30.
The probability of a tie is, P (T) = 0.10.
The sum of the probabilities of the outcomes of X are:
P (W) + P (L) + P (T) = 0.60 + 0.30 + 0.10 = 1.00
Thus, the distribution of W, L and T is a appropriate probability distribution.
(a)
Now, the outcomes W, L and T are one experiment.
The distribution of n independent and repeated trials, each having a discrete number of outcomes, each outcome occurring with a distinct constant probability is known as a Multinomial distribution.
The outcomes of X follows a Multinomial distribution.
The joint probability mass function of W, L and T is:
![P(W,\ L,\ T)={n\choose (n_(W)!* n_(L)!* n_(T)!)}* [P(W)]^{n_(W)}* [P(L)]^{n_(L)}* [P(T)]^{n_(T)}](https://img.qammunity.org/2021/formulas/mathematics/college/9xwrd4dnuk0hz6dnnaav7zujyu3b63d403.png)
The soccer tournament consists of n = 5 games.
Then the joint PMF of W, L and T is:
![P(W,\ L,\ T)={5\choose (n_(W)!* n_(L)!* n_(T)!)}* [0.60]^{n_(W)}* [0.30]^{n_(L)}* [0.10]^{n_(T)}](https://img.qammunity.org/2021/formulas/mathematics/college/ltzb567cm95gn2jol84duigbwodjfg3pq1.png)
(b)
The random variable W is defined as the number games won in the soccer tournament.
The probability of winning a game is, P (W) = p = 0.60.
Total number of games in the tournament is, n = 5.
A game is won independently of the others.
The random variable W follows a Binomial distribution.
The probability mass function of W is:
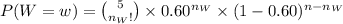
Thus, the marginal PMF of W is: