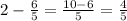Question

Please solve the problem with steps

Answer 1

HOPE YOU FOUND YOUR ANSWER

Explanation:

Answer 2

Infinite series equals 4/5

Explanation:

Notice that the series can be written as a combination of two geometric series, that can be found independently:

`(3^(n-1)-1)/(6^(n-1)) =(3^(n-1))/(6^(n-1)) -(1)/(6^(n-1)) =((1)/(2))^(n-1) -(1)/(6^(n-1))`

The first one:
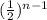`((1)/(2))^(n-1)` is a geometric sequence of first term (
`a_1`) "1" and common ratio (r) "
`(1)/(2)` ", so since the common ratio is smaller than one, we can find an answer for the infinite addition of its terms, given by:
`Infinite\,Sum=(a_1)/(1-r) = (1)/(1-(1)/(2) ) =(1)/((1)/(2) ) =2`

The second one:
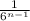`(1)/(6^(n-1))` is a geometric sequence of first term "1", and common ratio (r) "
`(1)/(6)` ". Again, since the common ratio is smaller than one, we can find its infinite sum:

`Infinite\,Sum=(a_1)/(1-r) = (1)/(1-(1)/(6) ) =(1)/((5)/(6) ) =(6)/(5)`

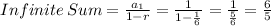
now we simply combine the results making sure we do the indicated difference: Infinite total sum=
`2-(6)/(5) =(10-6)/(5) =(4)/(5)`