Given that the length of the hypotenuse is 8 and the angle is 42°
The length of the one leg of the triangle is x.
We need to determine the value of x.
Value of x:
The value of x can be determined using the trigonometric ratio.
Thus, we have;
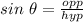
Substituting the values, we get;
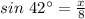
Multiplying both sides of the equation by 8, we get;
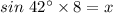
Simplifying, we get;
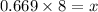
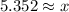
Therefore, the value of x is 5.35(app.)
Hence, Option A is the correct answer.