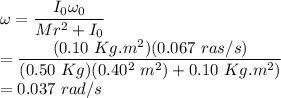Question

A solid disk rotates in the horizontal plane at an angular velocityof 0.067 rad/s with respect to an axis perpendicular to the disk atits center. The moment of inertia of the disk is 0.10 kgImage for A solid disk rotates in the horizontal plane at an angular velocityof 0.067 rad/s with respect to an axis perp m2. From above,sand is dropped straight down onto the rotating disk, so that athin uniform ring of sand is formed at a distance of 0.40 m fromthe axis. The sand in the ring has a mass of 0.50 kg. After all the sand is in place, what is the angular velocity of thedisk?

Answer 1

The angular velocity of the disk is
`\bf{0.037~rad/s}`.

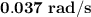Step-by-step explanation:

Given:

The angular velocity of the solid disk,
`\omega_(0) = 0.067~rad/s`

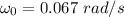
Moment of inertia of the disk,
`I_(0) = 0.10~Kg.m^(2)`

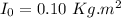
The radius of the sand ring,
`r = 0.40~m`

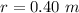
Mass of the sand disk,
`M = 0.5~Kg`.

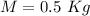From the conservation of angular momentum

`I\omega = I_(0)\omega_(0)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(1)`

Here,
`I` is the moment of inertia of the disk after the sand ring is formed and
`\omega` is the new angular velocity.

The new moment of inertia of the disk and sand ring is given by

`I = I_(r) + I_(0)\\= Mr^(2) + I_(0)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)`

Comparing equations (1) and (2), we have

`\omega = (I_(0)\omega_(0))/(Mr^(2) + I_(0))\\= ((0.10~Kg.m^(2))(0.067~ras/s))/((0.50~Kg)(0.40^(2)~m^(2)) + 0.10~Kg.m^(2)))\\= 0.037~rad/s`