Question

Kiwi fruits weight ~ The weight of Kiwi fruits is normally distributed with an average weight of 76 grams and a standard deviation of 3.6 grams.

What proportion of Kiwi fruits have weights between 70 and 80 grams? Enter your answer to 4 decimal places.

Answer 1

0.8190

Explanation:

The weight of Kiwi fruits is normally distributed with an average weight of 76 grams and a standard deviation of 3.6 grams.

We want to find the proportion of Kiwi fruits that have weights between 70 and 80 grams.

We find the z-scores of 70 and 80 using

`z = (x - \mu)/( \sigma)`

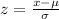
For 70, the z-score is:

`z = (70 - 76)/(3.6) = - 1.67`

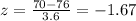
The area corresponding to a z-score of -1.67 on the standard normal distribution table is 0.0475

For 80, the z-score is:

`z = (80 - 76)/(3.6) = 1.11`

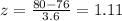
The area to the corresponding to a z-score of 1.11 is 0.8665

The area between the two z-scores is 0.8665-0.0475=0.8190

Therefore the proportion of Kiwi fruits have weights between 70 and 80 grams is 0.8190