Question

Find the intensity of a sound wave from 1km away, with a power of 20kw

Answer 1

`1.59\cdot 10^(-3) W/m^2`

Step-by-step explanation:

The intensity of a wave propagating in all directions from a source is given by the inverse square law:

`I=(P)/(4\pi r^2)`

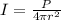
where

I is the intensity of the wave at a distance r from the source

P is the power of the source

r is the distance from the source

The formula arises from the fact that the wave propagates over the surface of a sphere of radius r, so over a surface of
`4\pi r^2` (surface of a sphere).

In this problem, we have:

`P=20 kW = 20,000 W` is the power of the source of the sound wave

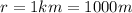`r=1 km = 1000 m` is the distance at which we want to calculate the intensity

Therefore, the intensity of the sound wave is:

`I=(20,000)/(4\pi (1000)^2)=1.59\cdot 10^(-3) W/m^2`