1 Answer

Pierre Henry · Answer 1 · 2021-12-08T19:12:32+0000

Given:

The given expression is
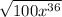
$\sqrt{100 x^(36)}$

We need to determine the simplified form of the expression.

Simplified form of the expression:

Let us determine the simplified form of the expression.

Applying the rule,
$\sqrt[n]{a b}=\sqrt[n]{a} \sqrt[n]{b}$

We get;

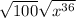
$√(100) \sqrt{x^(36)}$

Simplifying, we get;

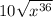
$10 \sqrt{x^(36)}$

Applying the exponent rule,
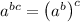$a^(b c)=\left(a^(b)\right)^(c)$ , we have;

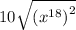
$10 \sqrt{\left(x^(18)\right)^(2)}$

Simplifying, we get;

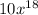
10 x^(18)

Thus, the simplified form of the expression is
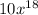
10 x^(18)

Hence, Option A is the correct answer.

Please log in or register to add a comment.