Question

Help for this math problem asap

Answer 1

Given:

It is given that the lines AB and DE are parallel.

We need to determine the value of x.

Value of x:

Let us use the property of similar triangles.

Thus, using the similar triangles, the corresponding sides of the triangle is given by

`(AB)/(ED)=(BC)/(CD)`

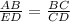
Substituting AB = 10, ED = 6, BC = 14 and CD = x in the above expression, we get;

`(10)/(6)=(14)/(x)`

Cross multiplying, we have;

`10x=14* 6`

`10x=84`

`x=8.4`

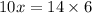
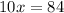
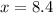
Thus, the value of x is 8.4