Question

you have enough tickets to play 6 different games at a amusement park. if there are 14 games, how many ways can you choose six? permutation or combination

Answer 1

3003 ways

Explanation:

You can basically choose 6 games from 14 games in total. This is essential a combination problem. We want the number of ways to choose 6 things from 14 things. The general formula for combinations is:

`nCr=(n!)/(r!(n-r)!)`

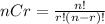
Which tells us the number of ways to choose "r" things from a total of "n" things.

The factorial notation is:

n! = n * (n-1) * (n-2) * ....

Example: 3! = 3 * 2 * 1

Now, we know from the problem,

n = 14

r = 6

So, substituting, we get:

`nCr=(n!)/(r!(n-r)!)\\14C6=(14!)/(6!(14-6)!)\\=(14!)/(8!*6!)\\=(14*13*12*11*10*9*8!)/(6!*8!)\\=(14*13*12*11*10*9)/(6*5*4*3*2*1)\\=3003`

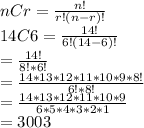
You can choose in 3003 ways