Question

A discriminant of -17 indicates what type of roots?

Answer 1

-17 has imaginary roots

Step-by-step explanation:

A discriminant of -17 indicates Imaginary (non-real) roots.

The discriminant of a polynomial equation is a value computed from the coefficients which helps us determine the type of roots it has - specifically whether they are real or non-real and distinct or repeated.

The discriminant indicated normally by Δ , is a part of the quadratic formula used to solve second degree equations.

Given a second degree equation in the general form:

a x² + bx + c = 0

The discriminant is:

Δ = b ² - 4ac

The discriminant can be used to characterize the solutions of the equation as:

1) Δ > 0 - two separate real solutions;

2) Δ = 0 - two coincident real solutions (or one repeated root);

3) Δ < 0 - no real solutions.

Answer 2

According to question D = -17 , i.e. D<0 . So , it's roots will be imaginary or complex roots !

Step-by-step explanation:

Here we need to tell , A discriminant of -17 indicates what type of roots . Let's find out:

For a general quadratic equation in form of
`f(x) = ax^2+bx+c` , Discriminant is given by :

⇒
`D = b^2-4ac`

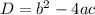
We have following 3 cases for discriminant as :

D>0

When discriminant is greater then zero we can say that , function has 2 roots which are distinct !

D=0

When discriminant is equal to zero , we can say that function has only one root !

D<0

When discriminant is less than zero we can say that the function has imaginary root or complex roots in form of
`a \pm ib` .

According to question D = -17 , i.e. D<0 . So , it's roots will be imaginary or complex roots !