Question

The function f(x) = x2 is transformed to f(x) = −1.4x2. Which statement describes the effect(s) of the transformation on the graph of the original function?

A) The parabola is wider and reflected across the x-axis.
B) The parabola is wider and reflected across the y-axis.
C) The parabola is narrower and reflected across the x-axis.
D) The parabola is narrower and reflected across the y-axis.

Answer 1

C) The parabola is narrower and reflected across the x-axis.

Explanation:

The original parabola has equation:

`f(x) = {x}^(2)`

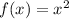
The transformed parabola has equation

`f(x) = - 1.4 {x}^(2)`

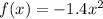
How wide the graph is can be determined by the absolute value of the coefficient.

The smaller the absolute value of the coefficient, the wider the graph.

Since

`|1| \: < \: | - 1.4|`

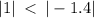
The original graph is wider than the transformed graph.

Also the negative factor tells us there is a reflection in the x-axis.