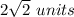Answer:
The lengths of the sides of the square base are
Explanation:
The correct question is
A triangular prism has an isosceles right triangular base with a hypotenuse of square root of 32 and a prism height of 12. a square prism has a height of 12 and its volume is equal to that of the triangular prism. what are the dimensions of the square base, in simplest radical form?
we know that
The volume of a prism is given by the formula
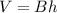
where
B is the area of the base
h is the height of the prism
so
If the volumes of the solids are the same and their heights are the same, then the area of the base of the triangular prism must be equal to the area of the base of the square prism
step 1
Find the area of the base of the triangular prism
Remember that in a right isosceles triangle, the two legs are equal
Let
x ---> the length side of each leg
Applying the Pythagorean Theorem
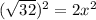
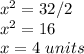
The area of the triangular base is equal to

step 2
Find the dimensions of base of the square prism
Let
b ---> the length side of the square base
The area of a square is given by the formula
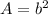
we have
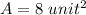 ----> is the same that the area of triangle
----> is the same that the area of triangle
substitute
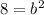
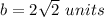
therefore
The lengths of the sides of the square base are