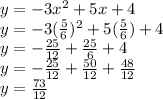Answer:
Axis of symmetry:
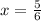
Vertex:
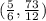
Explanation:
Recall that the formula for the axis of symmetry of a quadratic function of the form:
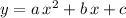 is that of a vertical line of the form
is that of a vertical line of the form
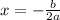
Since for our case,
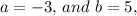 then the equation for the axis of symmetry is:
then the equation for the axis of symmetry is:
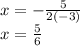
The horizontal (x) coordinate for the vertex is therefore 5/6, and the y coordinate can be obtained by replacing 'x" with the value "5/6" in the function's expression: