Question

On the first day of spring, an entire field of flowering trees blossoms. The population of locusts consuming these flowers rapidly increases as the trees blossom. The relationship between the elapsed time ttt, in days, since the beginning of spring, and the number of locusts, L(t)L(t)L, left parenthesis, t, right parenthesis, is modeled by the following function: L(t)=990⋅(1.47)t4.8 Complete the following sentence about the rate of change in the locust population. The population of locusts gains 47\%47%47, percent of its size every days.

Answer 1

4.8

Step-by-step explanation:

Answer 2

The population of locusts gains 47% of its size every 4.8 days.

Step-by-step explanation:

Just for better understanding, deleting the typos and arranging the garbled function, the text is:

The relationship between the elapsed time t, in days, since the beginning of spring, and the number of locusts, L(t), is modeled by the following function:

`L(t)=990(1.47)^(t/4.8)`

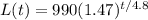
Analyze each part of the function:

• L(t) is the number of locusts (given)

• 990 is the initial value of the function, when t = 0 because, when t = 0 (1.47)⁰ = 1 and L(0) = 990.

• 1.47 is the growing factor: 1.47 = 1 + 0.47 = 1 + 47%. Thus, the growing factor is 47%.

• t is the the elapsed time in days (given): number of days since the spring began.

• The power, t/4.8, is the number of times the growing factor is applied to (mulitplied by) the initial number of locusts. If the number of days is 4.8 then t/4.8 = 4.8/4.8 = 1, meaning that the polulations of locusts grows 47% every 4.8 days.