Question

1.

(02.01 MC)
Triangle STU is located at S (2, 1), T (2, 3), and U (0, −1). The triangle is then transformed using the rule (x−4, y+3) to form the image S'T'U'. What are the new coordinates of S', T', and U'? (10 points)

Answer 1

Given that STU is a triangle located at S (2, 1), T (2, 3), and U (0, −1).

The triangle is then transformed using the rule
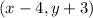`(x-4, y+3)` to form the image S'T'U'.

We need to determine new coordinates of S', T', and U'

Coordinates of S':

The coordinates of S' can be determined by substituting the coordinate (2,1) in the transformation rule
`(x-4, y+3)`

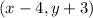
Thus, we have;

`S(x,y)\rightarrow (x-4, y+3)\rightarrow S'(x,y)`

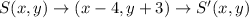
Substituting the coordinate (2,1), we get;

`S(2,1)\rightarrow (2-4, 1+3)\rightarrow S'(-2,4)`

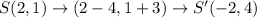
Therefore, the coordinates of the point S' is (-2,4)

Coordinates of T':

The coordinates of T' can be determined by substituting the coordinate (2,3) in the transformation rule
`(x-4, y+3)`

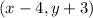
Thus, we have;

`T(x,y)\rightarrow (x-4, y+3)\rightarrow T'(x,y)`

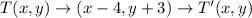
Substituting the coordinate (2,1), we get;

`T(2,3)\rightarrow (2-4, 3+3)\rightarrow T'(-2,6)`

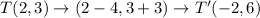
Therefore, the coordinates of the point T' is (-2,6)

Coordinates of U':

The coordinates of U' can be determined by substituting the coordinate (0,-1) in the transformation rule
`(x-4, y+3)`

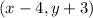
Thus, we have;

`U(x,y)\rightarrow (x-4, y+3)\rightarrow U'(x,y)`

Substituting the coordinate (2,1), we get;

`U(0,-1)\rightarrow (0-4, -1+3)\rightarrow U'(-4,2)`

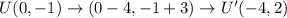
Therefore, the coordinates of the point U' is (-4,2)

Hence, the coordinates of S'T'U' are (-2,4), (-2,6) and (-4,2)