Question

Find the equation of the quadratic function f whose graph is shown below.

Answer 1

Explanation:

A quadratic function is a second-degree polynomial function with the general form

`f(x) \ = \ ax^(2) \ + \ bx \ + \ c`,

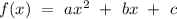where
`a`,
`b`, and
`c` are real numbers, and
`a \ \\eq \ 0`.

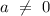The standard form or the vertex form of a quadratic function is, however, a little different from the general form. To get the standard form from the general form, we need to use the "complete the square" method.

`f(x) \ = \ ax^(2) \ + \ bx \ + \ c \\ \\ \\ f(x) \ = \ a\left(x^(2) \ + \ \displaystyle(b)/(a)x \right) \ + \ c \\ \\ \\ f(x) \ = \ a\left[x^(2) \ + \ \displaystyle(b)/(a)x \ + \ \left(\displaystyle(b)/(2a)\right)^(2) \ - \ \left(\displaystyle(b)/(2a)\right)^(2) \right] \ + \ c \\ \\ \\ f(x) \ = \ a\left[x^(2) \ + \ \displaystyle(b)/(a)x \ + \ \left(\displaystyle(b)/(2a)\right)^(2)\right] \ - \ a\left(\displaystyle(b)/(2a)\right)^(2) \ + \ c`

`f(x) \ = \ a\left(x \ + \ \displaystyle(b)/(2a)\right)^(2) \ + \ c \ - \ a\left(\displaystyle(b^(2))/(4a^(2))\right) \\ \\ \\ f(x) \ = \ a\left(x \ + \ \displaystyle(b)/(2a)\right)^(2) \ + \ c \ - \ \displaystyle(b^(2))/(4a)`

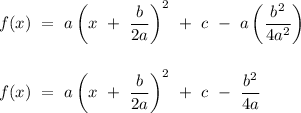
Let

`h \ = \ -\displaystyle(b)/(2a)` and
`k \ = \ c \ - \ \displaystyle(b^(2))/(4a)`,

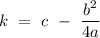then the expression reduces into

`f(x) \ = \ a \left(x \ - \ h\right)^(2) \ + \ k`,

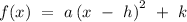where the point (h, k) are the coordinates for the vertex of the quadratic function.

There are two different methods to approach this question. First, we consider the general form of the quadratic function, it is observed that has a y-intercept at the point
`\left(0, \ 2\right)`, so

`f(0) \ = \ -2 \\ \\ \\ f(0) \ = \ a(0)^(2) \ + \ b(0) + c \\ \\ \\ c = \ -2`.

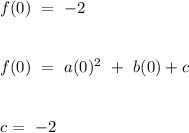Additionally, it is pointed that two distinct points
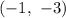`(-1, \ -3)` and
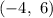`(-4, \ 6)` lies on the quadratic graph, hence

`f(-1) \ = \ -3 \\ \\ \\ f(-1) \ = \ a(-1)^(2) \ + \ b(-1) \ -2 \\ \\ \\ \-\hspace{0.36cm} -3 \ = \ a \ - \ b \ -2 \\ \\ \\ \-\hspace{0.3} a \ - \ b \ = \ -1 \ \ \ \ \ \ $-----$ \ (1)`

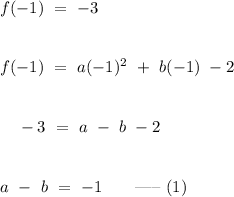
and

`\-\hspace{0.18cm}f(-4) \ = \ 6 \\ \\ \\ \-\hspace{0.18cm} f(-4) \ = \ a(-4)^(2) \ + \ b(-4) \ -2 \\ \\ \\ \-\hspace{0.97cm} 6 \ = \ 16a \ - \ 4b \ -2 \\ \\ \\ \-\hspace{0.98cm} 8 \ = \ 16a \ - \ 4b \\ \\ \\ 4a \ - \ b \ = \ 2 \ \ \ \ \ \ $-----$ \ (2)`.

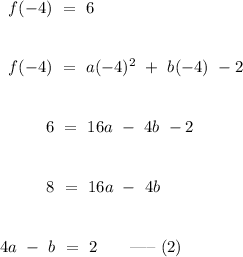Subtract equation (1) from equation (2) term-by-term,

`\-\hspace{0.72cm} (4a \ - \ b) \ - \ (a \ - \ b) \ = \ 2 \ - \ (-1) \\ \\ \\ (4a \ - \ a) \ + \ \left[-b \ - \ (-b)\right] \ = \ 2 \ + \ 1 \\ \\ \\ \-\hspace{3.8cm} 3a \ = \ 3 \\ \\ \\ \-\hspace{4cm} a \ = \ 1`

Substitute
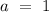`a \ = \ 1` into equation (1),

`1 \ - \ b \ = \ -1 \\ \\ \\ \-\hspace{0.86cm} b \ = \ 2`.

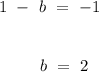Therefore, the equation of the quadratic function is

`f(x) \ = \ x^2 \ + \ 2x \ -2`.

`\rule{12.5cm}{0.02cm}`

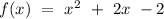Alternatively, the vertex of the quadratic function is given as the point
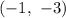`(-1, \ -3)`, substitute these coordinates into the vertex form of a quadratic function.

`f(x) = a\left(x \ + \ 1\right)^(2) \ - \ 3`.

Substitute the point
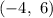`(-4, \ 6)` into the function above,

`f(-4) \ = \ 6 \\ \\ \\ f(-4) \ = \ a\left[(-4) \ + \ 1\right]^(2) \ - \ 3 \\ \\ \\ \-\hspace{0.75cm} 6 \ = \ a(-3)^(2) \ - \ 3 \\ \\ \\ \-\hspace{0.55cm} 9a \ = \ 9 \\ \\ \\ \-\hspace{0.75cm} a \ = \ 1`.

Therefore, the general form of the quadratic function is

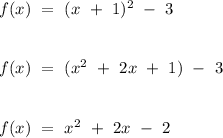`f(x) \ = \ (x \ + \ 1)^(2) \ - \ 3 \\ \\ \\ f(x) \ = \ (x^2 \ + \ 2x \ + \ 1) \ - \ 3 \\ \\ \\ f(x) \ = \ x^2 \ + \ 2x \ - \ 2`.