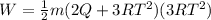Answer:
Work done is given as
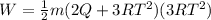
Step-by-step explanation:
As we know that the position of object is given as
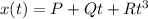
now we know that rate of change in position of object is known as velocity
so we have
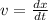
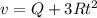
now we have
initial speed at t = 0
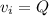
at t = T final speed is given as
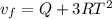
now work done is change in kinetic energy
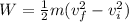
![W = (1)/(2)m[(Q + 3RT^2)^2 - Q^2]](https://img.qammunity.org/2021/formulas/physics/college/99kp8di1ilgvkjw8v3ecjx0qpxsl94xm92.png)