Question

4 points

A luminous source lights up an area 2.0 m away with an illuminance of
100.0 lx. How much will the illumination decrease by if the distance is
doubled? How much will the illumination decrease by if the distance is
tripled?

Answer 1

(a) 25lx

(b) 11.11lx

Step-by-step explanation:

Illuminance is inversely proportional to the square of the distance.

So,

`I = k(1)/(r^2)`

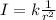
where, k is a constant

So,

(a)

If I = 100lx and r₂ = 2r Then,

`I_2 = k(1)/((2r)^2)`

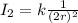
Dividing both the equation we get

`(I_1)/(I_2) = (k)/(r^2) X((2r)^2)/(k) \\\\(I_1)/(I_2) = 4\\\\I_2 = (I_1)/(4)\\\\I_2 = (100)/(4) = 25lx`

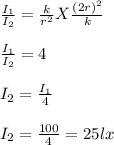
When the distance is doubled then the illumination reduces by one- fourth and becomes 25lx

(b)

If I = 100lx and r₂ = 3r Then,

`I_2 = k(1)/((3r)^2)`

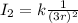
Dividing equation 1 and 3 we get

`(I_1)/(I_2) = (k)/(r^2) X((3r)^2)/(k) \\\\(I_1)/(I_2) = 9\\\\I_2 = (I_1)/(9)\\\\I_2 = (100)/(9) = 11.11lx`

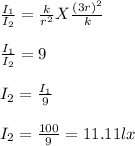
When the distance is tripled then the illumination reduces by one- ninth and becomes 11.11lx