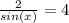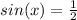Question

Given 1+cosx\sinx+sinx\1+cosx=4, find a numerical value of one trigonometric function of x.

Answer 1

D

Explanation:

guy above

Answer 2

Option d.
`sin(x)=(1)/(2)`

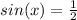
Explanation:

The complete question is

Given (1+cosx)/(sinx) + (sinx)/(1+cosx) =4, find a numerical value of one trigonometric function of x.

a. tanx=2

b. sinx=2

c. tanx=1/2

d. sinx=1/2

we have

`(1+cos(x))/(sin(x))+(sin(x))/(1+cos(x))=4`

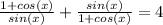
Find the common denominator and adds the fractions

`((1+cos(x))^2+sin^2(x))/((1+cos(x))sin(x))=4`

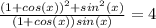
Expanded the numerator

`((1+2cos(x)+cos^2(x)+sin^2(x))/((1+cos(x))sin(x))=4`

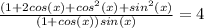
Remember that

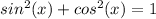`sin^2(x)+cos^2(x)=1` ----> trigonometric identity

substitute

`(1+2cos(x)+1)/((1+cos(x))sin(x))=4`

`(2+2cos(x))/((1+cos(x))sin(x))=4`

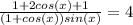
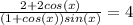
Factor 2 in the numerator

`(2(1+cos(x)))/((1+cos(x))sin(x))=4`

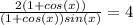
Simplify

`(2)/(sin(x))=4`

`sin(x)=(1)/(2)`