Answer:
p=0.3446
Explanation:
-Let Y be the random variable with parameter
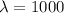 .
.
-The probability mass function is given as:

We set T=10, and calculate the probability as
![P(Y>10040)=1-P(Y\leq 10040)\\\\=1-P[(Y-10000)/(√(10000))\leq (10040-10000)/(100)]\\\\=1-P(Y\leq 0.4)\\\\=1-0.65542\\\\=0.34458](https://img.qammunity.org/2021/formulas/mathematics/college/he16l9tkg5iswlzgyy6tha18og1r1cn4dg.png)
Hence, the probability that 10 squared centimeters of dust contains more than 10040 particles is 0.3446