Question

A random sample of 21 observations is used to estimate the population mean. The sample mean and the sample standard deviation are calculated as 137.6 and 20.60, respectively. Assume that the population is normally distributed. Use Table 2.

a. Construct the 95% confidence interval for the population mean. (Round intermediate calculations to 4 decimal places. Round "f value to 3 decimal places and final answers to 2 decimal places.)
b. Construct the 99% confidence interval for the population mean. (Round intermediate calculations to 4 decimal places. Round "f* value to 3 decimal places and final answers to 2 decimal places.)
c. Use your answers to discuss the impact of the confidence level on the width of the interval. As the confidence level increases, the interval becomes wider. As the confidence level increases, the interval becomes narrower.

Answer 1

a. CI=[128.79,146.41]

b. CI=[122.81,152.39]

c. As the confidence level increases, the interval becomes wider.

Explanation:

a. -Given the sample mean is 137.6 and the standard deviation is 20.60.

-The confidence intervals can be constructed using the formula;

`\bar X\pm \ z(s)/(√(n)),`

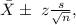
where:

• 
  `s` is the sample standard deviation
• 
  `z` is the s value of the desired confidence interval

we then calculate our confidence interval as:

`\bar X\pm z(s)/(√(n))\\\\=137.60\pm z_(0.05/2)*(20.60)/(√(21))\\\\=137.60\pm1.960* (20.60)/(√(21))\\\\=137.60\pm8.8108\\\\\\=[128.789,146.411]`

Hence, the 95% confidence interval is between 128.79 and 146.41

b. -Given the sample mean is 137.6 and the standard deviation is 20.60.

-The confidence intervals can be constructed using the formula in a above;

`\bar X\pm z(s)/(√(n))\\\\=137.60\pm z_(0.01/2)*(20.60)/(√(21))\\\\=137.60\pm3.291* (20.60)/(√(21))\\\\=137.60\pm 14.7940\\\\\\=[122.806,152.394]`

Hence, the variable's 99% confidence interval is between 122.81 and 152.39

c. -Increasing the confidence has an increasing effect on the margin of error.

-Since, the sample size is particularly small, a wider confidence interval is necessary to increase the margin of error.

-The 99% Confidence interval is the most appropriate to use in such a case.