Answer:
50% if light is unpolarized
100% if light is horizontally polarized
0% if light is vertically polarized
Step-by-step explanation:
A polarizer has an axis that "blocks" the component of light in the direction perpendicular to the direction of the polarizer axis.
When unpolarized light passes through a polarizer, the intensity of light is reduced to
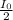 , where
, where
 is the initial intensity of the light: this is because only the component of the light parallel to the axis of the polarizer will pass through, and this component makes 1/2 of the incident light intensity. In this case, since the axis of the polarizer is horizontal, only the horizontal component of the light will pass through, while the vertical component will be blocked. So in this case the final intensity will be 50% of the initial one.
is the initial intensity of the light: this is because only the component of the light parallel to the axis of the polarizer will pass through, and this component makes 1/2 of the incident light intensity. In this case, since the axis of the polarizer is horizontal, only the horizontal component of the light will pass through, while the vertical component will be blocked. So in this case the final intensity will be 50% of the initial one.
On the other hand, if the incoming light is already horizontally polarized (same orientation as the polarizers), there is no vertical component to block, so all the light passes through the polarizer; therefore, the final intensity will be 100% of the original intensity.
Finally, if the incoming light is vertically polarized, no light will pass through it, because the polarizer's axis is horizontal, so it will block all the vertically polarized light: so the final intensity will be 0% of the original intensity.
All of this is after passing the 1st polarizer; so, after passing the 1st polarizer, the light is now horizontally polarized. Then, the intensity of the light passing through the 2nd polarizer is given by Malus' Law:
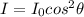
where
 is the angle between the axes of the two polarizers. Since here the two polarizers axes are parallel to each other,
is the angle between the axes of the two polarizers. Since here the two polarizers axes are parallel to each other,
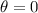 , so
, so
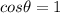 , and so the intensity after the 2nd polarizer is exactly the same as the intensity after the 1st polarizer.
, and so the intensity after the 2nd polarizer is exactly the same as the intensity after the 1st polarizer.