Question

The parallelogram shown below has an area of 212121 units^2

2
squared.
Find the missing height.

Answer 1

3 is the missing height. Khan sent me

Answer 2

In this context, the missing height measures 7 units

Step-by-step explanation:

The diagram for this problem is shown below. We know that a parallelogram is a quadrilateral where both pairs of opposite sides are parallel. The area (A) for any parallelogram is defined as:

`A=B* H \\ \\ \\ Where: \\ \\ B:Base \ of \ the \ parallelogram \\ \\ H:height \ of \ the \ parallelogram`

From the figure, we know:

`B=3units`

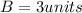
And the statements tells us that the area is:

`A=21units^2`

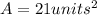
So, substituting in our equation for the are:

`21=3H \\ \\ \\ Isolating \ H: \\ \\ H=(21)/(3) \\ \\ \boxed{H=7units}`

So in this context, the missing height measures 7 units