Answer:
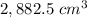
Explanation:
we know that
The approximate volume of the finished cylinder, is equal to subtract the volume of the hole from the volume of the original cylinder
so
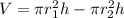
![V=\pi h[r_1^(2)-r_2^(2)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/21x0okimd05r4r1g3z0iyplnq85p8otn12.png)
where
r_1 is the radius of the original cylinder
r_2 is the radius of the hole
we have
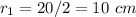 ---> the radius is half the diameter
---> the radius is half the diameter
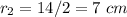 ---> the radius is half the diameter
---> the radius is half the diameter
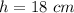
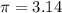
substitute the given values in the formula
![V=(3.14)(18)[10^(2)-7^(2)]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/5j4xmxvprh9nosqcmszjyyqzuo0w6b6hxq.png)
![V=56.52[51]\\V=2,882.5\ cm^3](https://img.qammunity.org/2021/formulas/mathematics/middle-school/fcoin6l155slzuwy0axa0mzbc7mktkrrsp.png)