Question

How many real solutions does 2x^2-4x+3=5

Answer 1

Explanation:

To find how many real solutions it has you have to find the solutions.

The quadratic formula is x=
`\frac{-b±\sqrt{b^(2)-4ac } }{2a}`

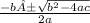
(the A with a weird line over it shouldn't be there but i cant get rid of it)

for the equation you gave me, you subtract 5 from both sides so it is equal to 0. It should be:

`2x^(2) -4x-2`

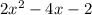
This equation is now in the format:

`ax^(2) +bx+c`

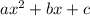
Now plug in what you have for a, b, and c (a= 2, b= -4, c= -2)

This will give you:

`x=\frac{-(-4)±\sqrt{(-4)^(2)-4(2)(-2) } } {2(2)}`

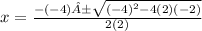
(again ignore that letter)

Now simplify it to:

`x=\frac{4±√((16-(-16) ) } {4}`

`x=\frac{4±√(32) } {4}`

`x=\frac{4±4√(2) } {4}`

`x=1±√(2)`

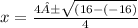
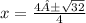
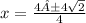
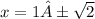
There are 2 real solutions because 1 plus the square root of 2 and 1 minus the square root of two are both real. (If it was 1 plus or minus the square root of a negative number it would be 0 real solutions because you cant take the square root of a negative number)

Sorry if this is confusing