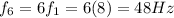Question

If a wave's third harmonic has a frequency of 24 Hz, what is its

natural (fundamental) frequency and what is the frequency of H6?

Answer 1

8 Hz, 48 Hz

Step-by-step explanation:

The standing waves on a string (or inside a pipe, for instance) have different modes of vibrations, depending on how many segments of the string are vibrating.

The fundamental frequency of a standing wave is the frequency of the fundamental mode of vibration; then, the higher modes of vibration are called harmonics. The frequency of the n-th harmonic is given by

`f_n = nf_1`

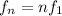
where

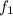`f_1` is the fundamental frequency

In this problem, we know that the wave's third harmonic has a frequency of

`f_3=24 Hz`

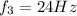
This means this is the frequency for n = 3. Therefore, we can find the fundamental frequency as:

`f_1=(f_3)/(3)=(24)/(3)=8 Hz`

Now we can also find the frequency of the 6-th harmonic using n = 6:

`f_6 = 6 f_1 = 6 (8)=48 Hz`