Question

THIRTY POINTS!

Shane plans to paint his barn. He will paint the 4 rectangular sides: left, right, front including the door, and back. He will also paint the 2 triangular sections formed by the roof with a height of 8 ft. He will not paint the 2 rectangular sections of the roof. Calculate the total number of square feet of surface area that Shane will paint

Answer 1

2972 square feet

Explanation:

2972 square feet

Answer 2

The 2972 square feet of surface area that Shane will paint, if he will paint the 4 rectangular sides, 2 triangular pieces and he will not paint the rectangular sections of roof.

Explanation:

The given is,

Shane wants to paint,

4 rectangular sides

2 triangular sides

Step:1

From the given diagram,

Total surface area of paint = (4 Rectangular sides surface ares) +

(2 triangular sides surface area)....(1)

Step:2

Surface area of 4 rectangular sides,

For Left side(rectangle) surface area,

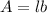`A =lb`...........................................................(2)

From the given diagram.

= (45.5 × 20)

= 910 Square feet

Dimensions of left side and right side are equal, so area of right side equal to the left side.

Area of right side = 910 square feet

Area of left and right sides,

= Left side area+ Right side area

= 910 + 910

= 1820 square feet

For front side area,

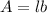`A =lb`...........................................................(3)

From the given diagram,

= (24 × 20 )

= 480 square feet

Dimensions of front side and back sides are equal, so area of front side equal to the back side.

Area of front side = 480 square feet

Area of front and back sides,

= front side area+ back side area

= 480 + 480

= 960 square feet

Surface area of rectangular sides,

= Area of left and right sides + Area of front and back sides

= 1820 + 960 = 2780 square feet

Step:3

Surface area of 2 triangular faces,

For area of triangular sides,

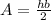`A = (hb)/(2)`...............................................(4)

From the given values,

=
`((8)(24))/(2)`

=
`(192)/(2)`

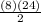
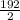
= 96 square feet

Dimensions of front side triangle and back side triangles are equal, so area of front side triangle equal to the back side triangle.

Area of front side triangle = 96 square meters

Area of front and back side triangles,

= front side triangle area+ back side triangle area

= 96 + 96

= 192 square feet

Step:4

From the equation (1),

Total surface area of paint = 2780 + 192

Total surface area of paint = 2972 square feet

Result:

The 2972 square feet of surface area that Shane will paint, if he will paint the 4 rectangular sides, 2 triangular pieces and he will not paint the rectangular sections of roof.