Given:
A tee box is 128 feet above its fairway. When a golf ball is hit from the tee box with an initial vertical velocity of 32 ft/s, the quadratic equation
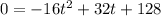 gives the time in seconds when a golf ball is at height 0 feet on the fairway.
gives the time in seconds when a golf ball is at height 0 feet on the fairway.
We need to determine the time that ball is in the air.
Time taken:
The time can be determined by factoring the quadratic equation.
Thus, we have;
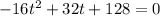
Let us solve the equation using the quadratic formula,
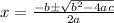
Substituting
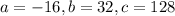 in the above formula, we get;
in the above formula, we get;
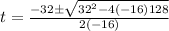
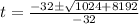


Thus, the roots of the equation are
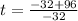 and
and
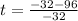
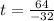 and
and
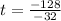
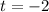 and
and
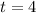
Since, the value of t cannot be negative, thus, the value of t is
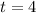
Hence, the ball is in the air for 4 seconds.