Answer:
There are two possible solutions to this equation:
x = 0, x= 5
Explanation:
starting with the given equation, multiply both sides by "2" to get rid of the denominator:
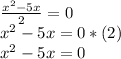
Then extract "x" as a common factor on the left side.
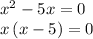
Notice that now you have a product of two factors [x is one, and the binomial (x-5) the other one] that equal zero. For such to happen, either factor must be zero. That is: x = 0, or (x-5) = 0.
So x=0 is a solution (renders 0 = 0 in the original equation)
The same is true for x = 5, it renders 0 = 0 in the original equation.