Question

What is the length of the apothem of a regular hexagon with 10-cm sides?

Answer 1

The length of apothem of given hexagon is 8.66 cm

Explanation:

Apothem of a polygon is given by:

`apothem = (s)/(2\ tan\ ((180)/(n)))`

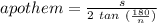
Here

s is length of side

tan is trigonometric function

and n denotes number of sides

Given that the polygon is a hexagon

`s = 10cm\\n = 6`

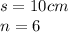
Putting the values in the formula

`apothem = (10)/(2\ tan\ ((180)/(6)))\\= (10)/(2\ tan\ 30)\\=(10)/(2 * 0.5773)\\=(10)/(1.1546)\\=8.6610\\Rounding\ off\ to\ nearest\ hundredth\\= 8.66\ cm`

Hence,

The length of apothem of given hexagon is 8.66 cm