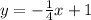Answer:
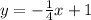
Explanation:
Since they give you two points on the lane (-4,2) and (4,0), the line can be determined by using them to find:
1) the slope of the line via the formula:
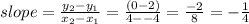
2) the line's y-intercept (b) requiring that one of the points satisfies the general equation of the line with the slope found above:
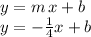
For example using point (4,0) in the equation above:
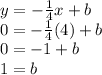
So the equation of the line through those points in slope intercept form is: