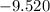Question

G(x)=12x2+5x−9 Which function has the lesser minimum? Show all your work.

Answer 1

Lesser minimum value of this function
`g(x) = 12x^(2) + 5x-9` is
`-9.520`

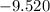
Explanation:

Given that,

It is a Quadratic function
`g(x) = 12x^(2) + 5x-9` .

To find :- Which function has lesser minimum ?

From the Question,

The General form of quadratic function is

`y = ax^(2) + bx + c`

Now comparing the given function we get

a = 12, b = 5, c = -9

So, finding the lesser minimum using the above quadratic function we have

Equation of lesser minimum =
`c - (b^(2) )/(4a)`

=
`-9 - (5^(2) )/(4* 12)`

=
`-9-(25)/(48)`

=
`-9.520`

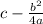
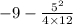
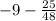
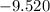
Hence,

We get the lesser minimum value of this function
`g(x) = 12x^(2) + 5x-9` is
`-9.520`