Question

Let H be the set of all vectors of the form .a 3b; b a; a; b/, where a and b are arbitrary scalars. That is, let H D f.a 3b; b a; a; b/ W a and b in Rg. Show that H is a subspace of R

Answer 1

H is the span of the vectors (1,-1,1,0), (-3,1,0,1).

Explanation:

To begin with remember the following theorem.

Theorem : Given a vector space V let
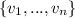`\{v_1 , ...,v_n\}` be a set of vectors of the , then
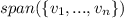`span(\{v_1 , ...,v_n\})` is a subspace of V.

Notice that any vector, in the described subspace looks like this.

(a-3b , b-a , a , b ) = (a , -a , a , 0 ) + ( -3b , b , 0 , b )

= a( 1 , -1 , 1 , 0 ) + b( -3 , 1 , 0 , 1 )

Therefore H is the span of the vectors (1,-1,1,0), (-3,1,0,1) and according to the theorem it would be a subspace.