Question

Two bicycle tires are set rolling with the same initial speed of 4.00 m/s along a long, straight road, and the distance each travels before its speed is reduced by half is measured. One tire is inflated to a pressure of 40 psi and goes a distance of 17.9 m ; the other is at 105 psi and goes a distance of 92.0 m . Assume that the net horizontal force is due to rolling friction only and take the free-fall acceleration to be g

Answer 1

The coefficient of rolling friction for the tire under low pressure is 0.0342.

Step-by-step explanation:

Two bicycle tires are set rolling with the same initial speed of 4.00 m/s

Final speed of both the bicycle, speed is reduced by half is measured, v = 2 m/s.

Here,

`u_kmg = ma\\\\a=\mu g`

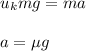
Using third equation of motion as :

`v^2-u^2=2as\\\\v^2-u^2=2\mu gs\\\\\mu =(v^2-u^2)/(2gs)\\\\\mu =(4^2-2^2)/(2* 9.8* 17.9)\\\\\mu=0.0342`

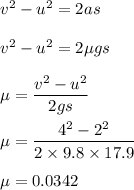
So, the coefficient of rolling friction for the tire under low pressure is 0.0342.