Question

The length of a rectangle is 3/2 units greater than twice its width. If its width is w, which expression gives the perimeter of the rectangle in terms of w?

Answer 1

`6w+3`

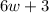
Explanation:

Given:

The length of a rectangle is 3/2 units greater than twice its width.

If its width is w

Question asked:

Which expression gives the perimeter of the rectangle in terms of w?

Solution:

Width of rectangle =
`w`

As given that the length of a rectangle is 3/2 units greater than twice its width.

Length of rectangle =
`2w+(3)/(2)`

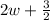
Now, as we know:

`Perimeter\ of\ rectangle=2(length +breadth)`

`=2(2w+(3)/(2) +w)\\\\ =2(3w+(3)/(2))\\ \\ =6w+(6)/(2) \\ \\ =6w+3`

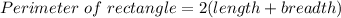
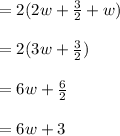
Therefore, perimeter of the rectangle in terms of w is
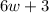`6w+3`.