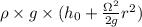Answer:
(a) The shape of the free surface of the water is a parabola of revolution as follows;
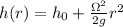
(b) The water pressure distribution over the bottom of the vessel is
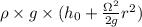 where r is the distance from the axis.
where r is the distance from the axis.
Step-by-step explanation:
To solve the question, we solve the Euler's equation of the form
 ω) = -ρu×ω =
ω) = -ρu×ω =
 (P +
(P +
 ρ ║u║²) + ρg
ρ ║u║²) + ρg
When in uniform rotation, we have
u =
 , ω =
, ω =
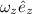 where
where
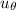 = rΩ and
= rΩ and
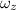 = 2Ω
= 2Ω
Therefore, u × ω = 2·r·Ω²·
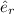
From which the radial component of the vector equation is given as
-2·p·r·Ω² =
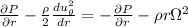
Therefore,
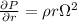 =
=
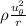
Integrating gives
P(r, z) =
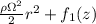
By substituting the above into the z component of the equation of motion, we obtain;
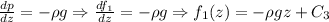
Therefore
P(r, z) =
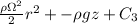
From the boundary conditions r = R and z =
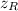 , we find C₃ as follows
, we find C₃ as follows
P(r = R, z =
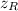 ) =
) =
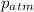
Therefore
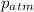 =
=
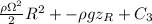
From which we have
P(r, z) -
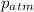 =
=
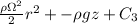 -
-
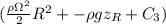
P(r, z) -
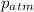 =
=
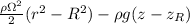
We note that at the surface, the interface between the air and the liquid
P =
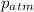 , the shape of the of the free surface of the water is therefore;
, the shape of the of the free surface of the water is therefore;
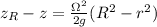 ,
,
Given that at r = 0 we have the height = h₀
Therefore,
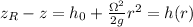
The shape of the of the free surface of the water is a parabola of revolution.
(b) The water pressure distribution over the bottom of the vessel is given by
ρ × g × z
=
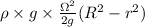 =
=