Answer:
Fifth Day (1024 pounds)
Explanation:
For every subsequent day, he collected 4 times the previous day.
This increase is a ratio/product, therefore the sequence is a geometric sequence.
The nth term of a geometric sequence,
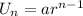
Where:
a=first term
r=common ratio
n=number of terms
Corey collected 4 pounds of newspaper on day 1., a=4
After day one he collected 4 times the amount and for every subsequent day, he collected 4 times the previous day. r=4
We want to determine on which day he will first collect over a 1000 pounds of new paper.
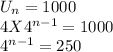
In order to apply law of indices, we look for the next term greater than 250 which is an index of 4.
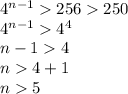
Therefore on the fifth day, he will collect an amount over 1000 pounds, precisely 1024 pounds.