Question

A, B, and C are collinear, and B is between A and C. The ratio of AB to AC is 1:2 If A is at (6,3) and B is at (-1,2), what are the coordinates of point C?

Answer 1

The coordinates of C is (-8,1)

Explanation:

Looking at the attached image, you'd see that, AB is 1 and BC is 1, that's because we are told that ratio of AB to AC is 1:2 meaning, AC is 2 and AB is 1. Therefore for that ratio to be satisfied BC has to be 1 so that AC would be 2.

Now let's assume the coordinates of C is
`(x,y)`.

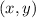To get it's coordinates, we use the section formula:

`(x,y)= ((mx + nx_(1))/(m + n) , (my + ny_(1))/(m + n))`

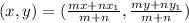
Where (m,n) is the (AB, BC)

Therefore we have

`(-1,2) = ((1* x + 1*6)/(1 + 1) , (1* y + 1*3)/(1 + 1))`

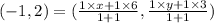
This gives:

`(-1,2) = ((x + 6)/(2) , (y + 3)/(2))`

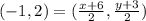
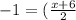`-1 =( (x + 6)/(2)` and
`2 = (y + 3)/(2))`

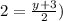
From there x = -8 and y = 1

Therefore the coordinates of C is (-8, 1).