Question

Assume that 74% of randomly selected adults have a credit card. Assume that a group of five adults is randomly selected. If the group of five adults includes exactly 1 with a credit card, is that value of 1 significantly low

Answer 1

Yes, value of adults having exactly 1 credit card is significantly low.

Explanation:

We are given that 74% of randomly selected adults have a credit card. Assume that a group of five adults is randomly selected.

And we have to check that if the group of five adults includes exactly 1 with a credit card, is that value of 1 significantly low or not.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

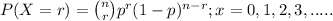
where, n = number of trials (samples) taken = 5 adults

r = number of success = exactly 1

p = probability of success which in our question is % of adults

having a credit card, i.e; 74%

LET X = Number of adults having a credit card

So, it means X ~
`Binom(n=5, p=0.74)`

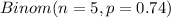
Now, Probability that the group of five adults includes exactly 1 with a credit card is given by = P(X = 1)

P(X = 1) =
`\binom{5}{1}* 0.74^(1)* (1-0.74)^(5-1)`

=
`5 * 0.74 * 0.26^(4)`

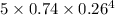
= 0.0169

So, the probability that in a group of five adults, exactly 1 have a credit card is 0.0169 or 1.69%.

Now, for any probability value to be significantly low it must be less than 5% as it is considered very unusual or may be called it that the probability of happening of that event is very rare or low.

Since, here our probability is way less than 5% i.e. 1.69%. So we can conclude that the value of adults having exactly 1 credit card in a group of 5 is significantly very low.