Answer:
For making this statement true we have to check Triangle Inequality theorem.
Explanation:
Given that,
Triangle ΔABC having three vertices are A (
 ), B(
), B(
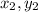 ), C (
), C (
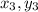 ) and AC is the longest side.
) and AC is the longest side.
from the question,
Diagram of the given scenario is shown below,
According to Triangle Inequality theorem states that sum of any 2 sides of a triangle is always greater than third side.
Taking the ΔABC we have,
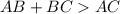
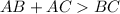
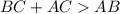
This condition must be satisfied for drawing a triangle if any two side sum is lesser than third side it will not form a triangle.
Hence,
For making this statement true we have to check Triangle Inequality theorem.