Answer: He should include 720 hard drives in his new sample.
Explanation:
- Margin of error is inversely proportional to the square root of the sample size.
Let E be the margin of error and n be the sample size , then 4
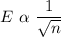
Also, by equation of inverse variation , we have
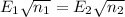
Put
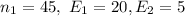 (given) , we get
(given) , we get
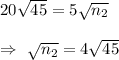
Taking square on both sides , we get
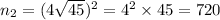
Hence, he should include 720 hard drives in his new sample.