Answer:
The required work to empty the the tank is 247401 J.
Step-by-step explanation:
Given that,
A tank is in the shape of right circular cone.
The radius of the tank= 2 m
The height of the tank = 4 m
The relation between the radius and the height is
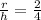

Let h be the height of hot of chocolate any time t.
The volume of a cone is
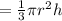
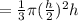
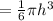
The volume of the chocolate is
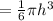
The mass of the chocolate is(M)= Density × Volume
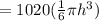 Kg
Kg
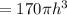 kg
kg
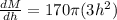
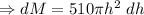
Work done = Force × displacement
= Mass × acceleration×displacement
Here acceleration= acceleration due to gravity = 9.8 m/s²
The displacement when the hot chocolate level is h is = (4-h)
Work done (dw)

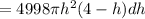
Work done = W

![=\int_0^34998\pi [4h^2-h^3]dh](https://img.qammunity.org/2021/formulas/physics/high-school/nozgvao2njmrv23a6oztd24lca9smn4p0t.png)
![=4998\pi [4(h^3)/(3)-(h^4)/(4)]_0^3](https://img.qammunity.org/2021/formulas/physics/high-school/12ihpqlzr2kbz9qwbhqpttmvfstj0y21mq.png)
![=4998\pi [(4(3^3)/(3)-(3^4)/(4))-(4(0^3)/(3)-(0^4)/(4))]](https://img.qammunity.org/2021/formulas/physics/high-school/47z0holqyopxprc4rowglqnrc40xuicecp.png)
=247401 J
The required work to empty the the tank is 247401 J.