Question

Amit solved the equation for x using the steps shown below. What was Amit's error? Amit should have multiplied both sides of the equation by . Amit should have multiplied both sides of the equation by . The product of and 420 is not equal to 175. The product of and –420 should have been the value of x.

Answer 1

Answer: The answer to your question will be D ( The product of 5/12 and -420 should have been the value of x )

Explanation:

I took the test on edg

Answer 2

(D) The product of
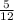`(5)/(12)` and –420 should have been the value of x.

Explanation:

The equation Amit was trying to solve is given as:

`(5)/(12)=-(x)/(420)`

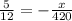
He uses the following steps:

`(5)/(12)\cdot 420=-(x)/(420)\cdot 420\\x=175`

We now consider the given options for his error.

Option A: Amit should have multiplied both sides of the equation by
`(5)/(12)`

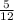
Option B: Amit should have multiplied both sides of the equation by
`(12)/(5)`

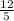
Options A and B are not viable as it only complicates the work.

Option C: The product of
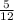`(5)/(12)` and 420 is not equal to 175.

The product of
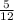`(5)/(12)` and 420 is equal to 175.

Option D: The product of
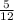`(5)/(12)` and –420 should have been the value of x.

From the steps: -x=175

Solved Correctly

`(5)/(12)\cdot -420=-(x)/(420)\cdot -420\\x=-175`

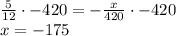
Therefore option D is the correct anser.