Answer:
3
Explanation:
Given:
If fifteen less than two times a number is divided by six more than the number, the result is four less than 9 times the reciprocal of the number.
Question asked:
Find the number ?
Solution:
Let the number be

As given that:-
15 less than 2 times a number
 6 more than the number = 4 less than 9 times the reciprocal of the number
6 more than the number = 4 less than 9 times the reciprocal of the number
Then the equation will be:-

By cross multiplication:-
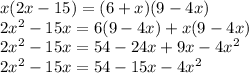
By adding both sides by

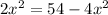
Adding both sides by
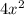
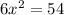
Dividing both sides by 6

Taking root both sides
![\sqrt[2]{x^(2) } =\sqrt[2]{9} \\x=\sqrt[2]{3*3} \\x=3](https://img.qammunity.org/2021/formulas/mathematics/high-school/v7pomqcxmwo93tyzqso32fn29cuolj3lkr.png)
Thus, the number is 3.